Pregel(图计算)
图计算简介
图结构数据:
许多大数据都是以大规模图或网络的形式呈现。
许多非图结构的大数据,也常常会被转换为图模型后进行分析。
图数据结构很好地表达了数据之间的关联性。
关联性计算是大数据计算的核心——通过获得数据的关联性,可以从噪音很多的海量数据中抽取有用的信息。
传统图计算解决方案的不足之处:
很多传统的图计算算法都存在以下几个典型问题:
常常表现出比较差的内存访问局部性
针对单个顶点的处理工作过少
计算过程中伴随着并行度的改变
针对大型图(比如社交网络和网络图)的计算问题,可能的解决方案及其不足之处具体如下:
为特定的图应用定制相应的分布式实现
基于现有的分布式计算平台进行图计算
使用单机的图算法库:比如BGL、LEAD、NetworkX、JDSL、Standford GraphBase和FGL等
使用已有的并行图计算系统:比如,Parallel BGL和CGM Graph,实现了很多并行图算法
图计算通用软件:
针对大型图的计算,目前通用的图计算软件主要包括两种:
第一种主要是基于遍历算法的、实时的图数据库,如Neo4j、OrientDB、DEX和 Infinite Graph。
第二种则是以图顶点为中心的、基于消息传递批处理的并行引擎,如GoldenOrb、Giraph、Pregel和Hama,这些图处理软件主要是基于BSP模型实现的并行图处理系统。
一次BSP(Bulk Synchronous Parallel Computing Model,块同步并行计算模型,又称“大同步”模型)计算过程包括一系列全局超步(所谓的超步就是计算中的一次迭代),每个超步主要包括三个组件:
局部计算:每个参与的处理器都有自身的计算任务。
通讯:处理器群相互交换数据。
栅栏同步(Barrier Synchronization):当一个处理器遇到“路障”(或栅栏),会等到其他所有处理器完成它们的计算步骤。
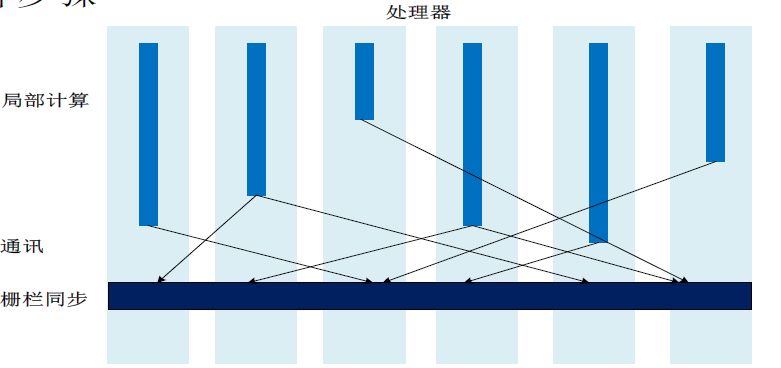
图:一个超步的垂直结构图
Pregel图计算模型
Pregel简介:
谷歌公司在2003年到2004年公布了GFS、MapReduce和BigTable
谷歌在后Hadoop时代的新“三驾马车”
Caffeine
Dremel
Pregel
Pregel是一种基于BSP模型实现的并行图处理系统。
为了解决大型图的分布式计算问题,Pregel搭建了一套可扩展的、有容错机制的平台,该平台提供了一套非常灵活的API,可以描述各种各样的图计算。
Pregel作为分布式图计算的计算框架,主要用于图遍历、最短路径、PageRank计算等等。
有向图和顶点:
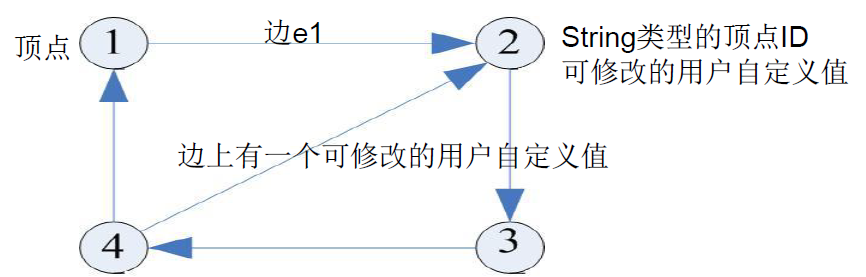
图:有向图和顶点
Pregel计算模型以有向图作为输入
有向图的每个顶点都有一个String类型的顶点ID
每个顶点都有一个可修改的用户自定义值与之关联
每条有向边都和其源顶点关联,并记录了其目标顶点ID
边上有一个可修改的用户自定义值与之关联
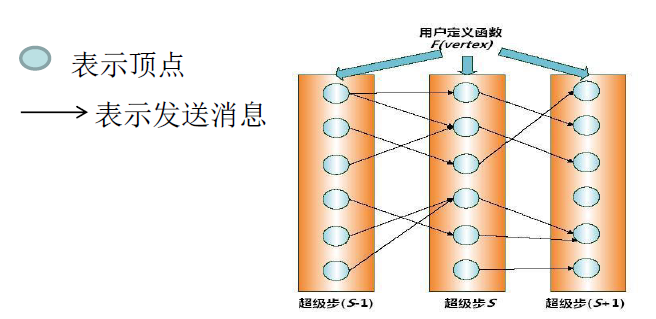
图:超步示意图
在每个超步S中,图中的所有顶点都会并行执行相同的用户自定义函数。
每个顶点可以接收前一个超步(S-1)中发送给它的消息,修改其自身及其出射边的状态,并发送消息给其他顶点,甚至是修改整个图的拓扑结构。
在这种计算模式中,“边。”并不是核心对象,在边上面不会运行相应的计算,只有顶点才会执行用户自定义函数进行相应计算。
顶点之间的消息传递:
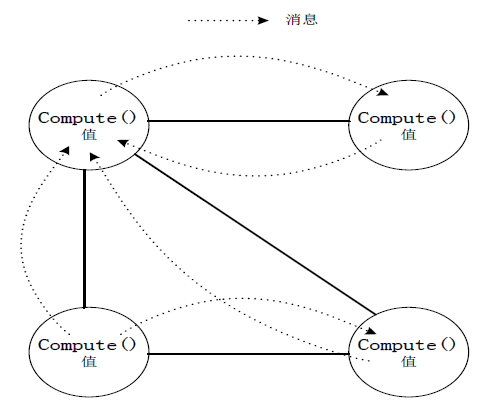
图:纯消息传递模型图
采用消息传递模型主要基于以下两个原因:
消息传递具有足够的表达能力,没有必要使用远程读取或共享内存的方式.
有助于提升系统整体性能.
Pregel的计算过程:
Pregel的计算过程是由一系列被称为“超步”的迭代组成的。
在每个超步中,每个顶点上面都会并行执行用户自定义的函数,该函数描述了一个顶点V在一个超步S中需要执行的操作。
该函数可以读取前一个超步(S-1)中其他顶点发送给顶点V的消息,执行相应计算后,修改顶点V及其出射边的状态,然后沿着顶点V的出射边发送消息给其他顶点,而且,一个消息可能经过多条边的传递后被发送到任意已知ID的目标顶点上去。
这些消息将会在下一个超步(S+1)中被目标顶点接收,然后像上述过程一样开始下一个超步(S+1)的迭代过程。
在Pregel计算过程中,一个算法什么时候可以结束,是由所有顶点的状态决定的。
在第0个超步,所有顶点处于活跃状态。
当一个顶点不需要继续执行进一步的计算时,就会把自己的状态设置为“停机”,进入非活跃状态。
当一个处于非活跃状态的顶点收到来自其他顶点的消息时,Pregel计算框架必须根据条件判断来决定是否将其显式唤醒进入活跃状态。
当图中所有的顶点都已经标识其自身达到“非活跃(inactive)”状态,并且没有消息在传送的时候,算法就可以停止运行。
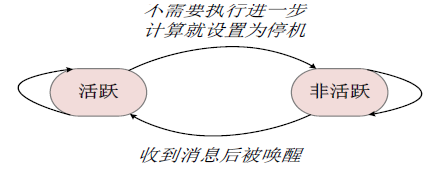
图:一个简单的状态机图
一个简单示例:
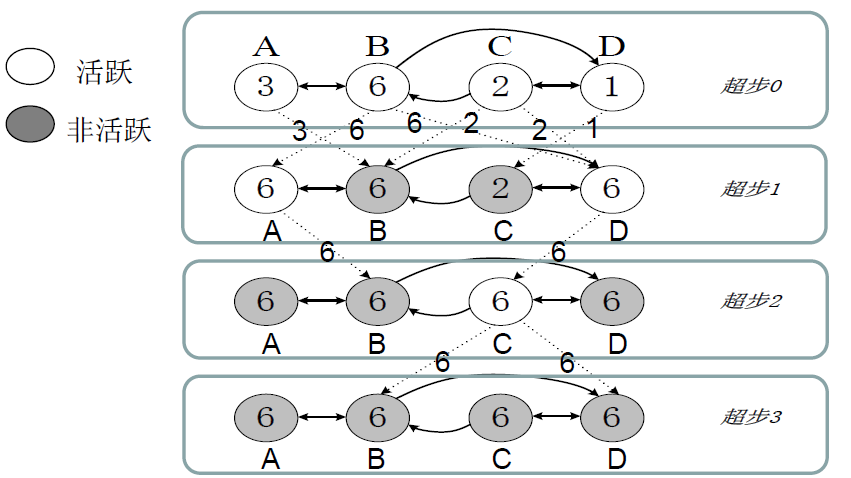
图:一个求最大值的Pregel计算过程图
Pregel的工作原理
Pregel的C++ API:
Pregel已经预先定义好一个基类——Vertex类:复制
在Vetex类中,定义了三个值类型参数,分别表示顶点、边和消息。每一个顶点都有一个给定类型的值与之对应。
编写Pregel程序时,需要继承Vertex类,并且覆写Vertex类的虚函数Compute()。
消息传递机制:
顶点之间的通讯是借助于消息传递机制来实现的,每条消息都包含了消息值和需要到达的目标顶点ID。用户可以通过Vertex类的模板参数来设定消息值的数据类型。
在一个超步S中,一个顶点可以发送任意数量的消息,这些消息将在下一个超步(S+1)中被其他顶点接收。
一个顶点V通过与之关联的出射边向外发送消息,并且,消息要到达的目标顶点并不一定是与顶点V相邻的顶点,一个消息可以连续经过多条连通的边到达某个与顶点V不相邻的顶点U,U可以从接收的消息中获取到与其不相邻的顶点V的ID。
Combiner:
Pregel计算框架在消息发出去之前,Combiner可以将发往同一个顶点的多个整型值进行求和得到一个值,只需向外发送这个“求和结果”,从而实现了由多个消息合并成一个消息,大大减少了传输和缓存的开销。
在默认情况下,Pregel计算框架并不会开启Combiner功能。
当用户打算开启Combiner功能时,可以继承Combiner类并覆写虚函数Combine()。
此外,通常只对那些满足交换律和结合律的操作才可以去开启Combiner功能。
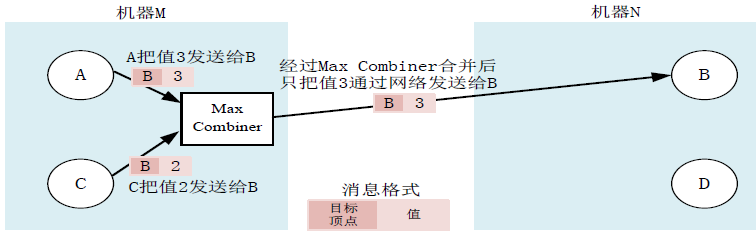
图:Combiner应用的例子
Aggregator:
Aggregator提供了一种全局通信、监控和数据查看的机制。
在一个超步S中,每一个顶点都可以向一个Aggregator提供一个数据,Pregel计算框架会对这些值进行聚合操作产生一个值,在下一个超步(S+1)中,图中的所有顶点都可以看见这个值。
Aggregator的聚合功能,允许在整型和字符串类型上执行最大值、最小值、求和操作,比如,可以定义一个“Sum”Aggregator来统计每个顶点的出射边数量,最后相加可以得到整个图的边的数量。
Aggregator还可以实现全局协同的功能,比如,可以设计“and” Aggregator来决定在某个超步中Compute()函数是否执行某些逻辑分支,只有当“and” Aggregator显示所有顶点都满足了某条件时,才去执行这些逻辑分支。
拓扑改变:
Pregel计算框架允许用户在自定义函数Compute()中定义操作,修改图的拓扑结构,比如在图中增加(或删除)边或顶点。
对于全局拓扑改变,Pregel采用了惰性协调机制。
对于本地的局部拓扑改变,是不会引发冲突的,顶点或边的本地增减能够立即生效,很大程度上简化了分布式编程。
输入和输出:
在Pregel计算框架中,图的保存格式多种多样,包括文本文件、关系数据库或键值数据库等。
在Pregel中,“从输入文件生成得到图结构”和“执行图计算”这两个过程是分离的,从而不会限制输入文件的格式。
对于输出,Pregel也采用了灵活的方式,可以以多种方式进行输出。
Pregel的体系结构
Pregel的执行过程:
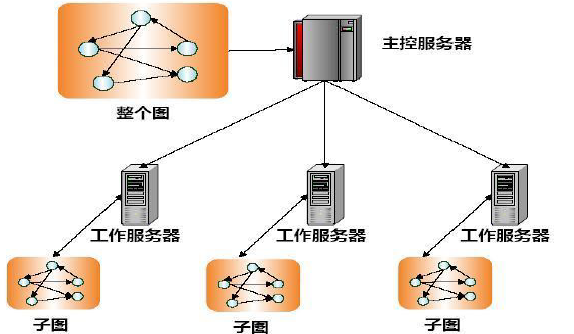
图:图的划分图
在Pregel计算框架中,一个大型图会被划分成许多个分区,每个分区都包含了一部分顶点以及以其为起点的边。
一个顶点应该被分配到哪个分区上,是由一个函数决定的,系统默认函数为hash(ID) mod N,其中,N为所有分区总数,ID是这个顶点的标识符;当然,用户也可以自己定义这个函数。
这样,无论在哪台机器上,都可以简单根据顶点ID判断出该顶点属于哪个分区,即使该顶点可能已经不存在了。

图:Pregel的执行过程
在理想的情况下(不发生任何错误),一个Pregel用户程序的执行过程如下:
选择集群中的多台机器执行图计算任务,有一台机器会被选为Master,其他机器作为Worker。
Master把一个图分成多个分区,并把分区分配到多个Worker。一个Worker会领到一个或多个分区,每个Worker知道所有其他Worker所分配到的分区情况。
Master会把用户输入划分成多个部分。然后,Master会 为每个Worker分配用户输入的一部分。如果一个Worker从输入内容中加载到的顶点,刚好是自己所分配到的分区中的顶点,就会立即更新相应的数据结构。否则,该Worker会根据加载到的顶点的ID,把它发送到其所属的分区所在的Worker上。当所有的输入都被加载后,图中的所有顶点都会被标记为“活跃”状态。
Master向每个Worker发送指令,Worker收到指令后,开始运行一个超步。当一个超步中的所有工作都完成以后,Worker会通知Master,并把自己在下一个超步还处于“活跃”状态的顶点的数量报告给Master。上述步骤会被不断重复,直到所有顶点都不再活跃并且系统中不会有任何消息在传输,这时,执行过程才会结束。
计算过程结束后,Master会给所有的Worker发送指令,通知每个Worker对自己的计算结果进行持久化存储。
容错性:
Pregel采用检查点机制来实现容错。在每个超步的开始,Master会通知所有的Worker把自己管辖的分区的状态写入到持久化存储设备。
Master会周期性地向每个Worker发送ping消息,Worker收到ping消息后会给Master发送反馈消息。
每个Worker上都保存了一个或多个分区的状态信息,当一个Worker发生故障时,它所负责维护的分区的当前状态信息就会丢失。Master监测到一个Worker发生故障“失效”后,会把失效Worker所分配到的分区,重新分配到其他处于正常工作状态的Worker集合上,然后,所有这些分区会从最近的某超步S开始时写出的检查点中,重新加载状态信息。
Worker:
在一个Worker中,它所管辖的分区的状态信息是保存在内存中的。分区中的顶点的状态信息包括:
顶点的当前值。
以该顶点为起点的出射边列表,每条出射边包含了目标顶点ID和边的值。
消息队列,包含了所有接收到的、发送给该顶点的消息。
标志位,用来标记顶点是否处于活跃状态。
在每个超步中,Worker会对自己所管辖的分区中的每个顶点进行遍历,并调用顶点上的Compute()函数,在调用时,会把以下三个参数传递进去:
该顶点的当前值
一个接收到的消息的迭代器
一个出射边的迭代器
在Pregel中,为了获得更好的性能,“标志位”和输入消息队列是分开保存的。
对于每个顶点而言,Pregel只保存一份顶点值和边值,但是,会保存两份“标志位”和输入消息队列,分别用于当前超步和下一个超步。
如果一个顶点V在超步S接收到消息,那么,它表示V将会在下一个超步S+1中(而不是当前超步S中)处于“活跃”状态。
当一个Worker上的一个顶点V需要发送消息到其他顶点U时,该Worker会首先判断目标顶点U是否位于自己机器上。
如果目标顶点U在自己的机器上,就直接把消息放入到与目标顶点U对应的输入消息队列中。
如果发现目标顶点U在远程机器上,这个消息就会被暂时缓存到本地,当缓存中的消息数目达到一个事先设定的阈值时,这些缓存消息会被批量异步发送出去,传输到目标顶点所在的Worker上。
Master:
Master的主要作用:
Master主要负责协调各个Worker执行任务,每个Worker会借助于名称服务系统定位到Master的位置,并向Master发送自己的注册信息,Master会为每个Worker分配一个唯一的ID。
Master维护着关于当前处于“有效”状态的所有Worker的各种信息,包括每个Worker的ID和地址信息,以及每个Worker被分配到的分区信息。
Master中保存这些信息的数据结构的大小,只与分区的数量有关,而与顶点和边的数量无关。
Master与Worker的交互:
一个大规模图计算任务会被Master分解到多个Worker去执行,在每个超步开始时,Master都会向所有处于“有效”状态的Worker发送相同的指令,然后等待这些Worker的回应。
如果在指定时间内收不到某个Worker的反馈,Master就认为这个Worker失效。
如果参与任务执行的多个Worker中的任意一个发生了故障失效,Master就会进入恢复模式。
在每个超步中,图计算的各种工作,比如输入、输出、计算、保存和从检查点中恢复,都会在“路障(barrier)”之前结束。
Master在内部运行了一个HTTP服务器来显示图计算过程的各种信息。用户可以通过网页随时监控图计算执行过程各个细节:
图的大小
关于出度分布的柱状图
处于活跃状态的顶点数量
在当前超步的时间信息和消息流量
所有用户自定义Aggregator的值
Aggregator:
每个用户自定义的Aggregator都会采用聚合函数对一个值集合进行聚合计算得到一个全局值。
每个Worker都保存了一个Aggregator的实例集,其中的每个实例都是由类型名称和实例名称来标识的。
在执行图计算过程的某个超步S中,每个Worker会利用一个Aggregator对当前本地分区中包含的所有顶点的值进行归约,得到一个本地的局部归约值。
在超步S结束时,所有Worker会将所有包含局部归约值的Aggregator的值进行最后的汇总,得到全局值,然后提交给Master。
在下一个超步S+1开始时,Master就会将Aggregator的全局值发送给每个Worker。
Pregel的应用实例—单源最短路径
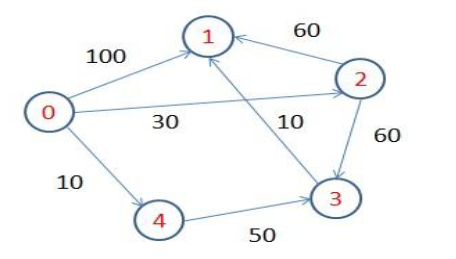
图:Dijkstra算法是解决单源最短路径问题的贪婪算法
Pregel非常适合用来解决单源最短路径问题,实现代码如下:复制
Hama简介
Hama概述:
Hama是Google Pregel的开源实现。
与Hadoop适合于分布式大数据处理不同,Hama主要用于分布式的矩阵、graph、网络算法的计算。
Hama是在HDFS上实现的BSP(Bulk Synchronous Parallel)计算框架,弥补Hadoop在计算能力上的不足。
Hama是基于BSP(BulkSynchronous Parallel)计算技术的并行计算框架,用于大量的科学计算(比如矩阵、图论、网络等)。BSP计算技术最大的优势是加快迭代,在解决最小路径等问题中可以快速得到可行解。同时,Hama提供简单的编程,比如flexible模型、传统的消息传递模型,而且兼容很多分布式文件系统,比如HDFS、Hbase等。用户可以使用现有的Hadoop集群进行Hama BSP.
现在Hama最新的版本为2012年6月31号发行的0.5.0.这是 Hama 做为 Apache 顶级项目后首次发布的版本,该版本包含两个显著的新特性,分别是消息压缩器和完整的 Google Pregel 克隆,另外在计算系统性能和可持续性上都得以提升。
Hama结构:
Hama主要有三部分构成:BSPMaster、GroomServers 和Zookeeper。与Hadoop结构很相似,但没有通信和同步机制的部分。
Hama的集群由一个BSPMaster和多个互不关联的GroomServer作计算结点组成,HDFS和Zookeeper都可以是独立的集群。启动从BSPMaster开始,如果是master会启动BSPMaster、GroomServer两个进程,如果只是计算结点则只会启动GroomServer,启动/关闭脚本都是Master机器远程在GroomServer机器上执行。
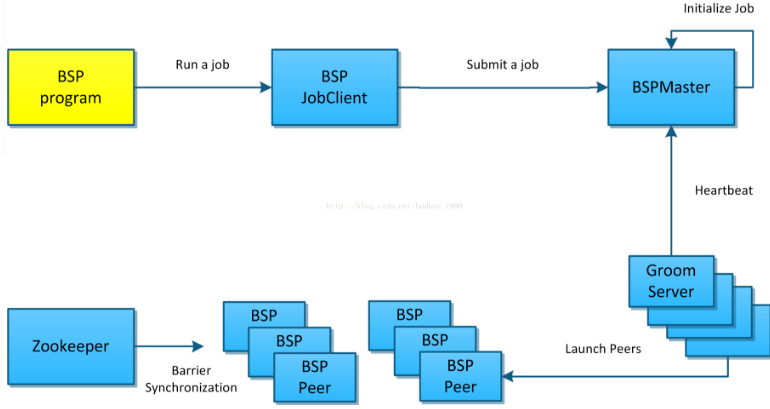
图:Hama体系结构
BSPMaster:
BSPMaster 即集群的主,负责了集群各GroomServer结点的管理与作业的调度,就我所知它还存在单点的问题。相当于Hadoop的JobTracker或HDFS的NameNode。其基本作用如下:
维持Groom服务器状态。
维护supersteps和集群中的计数器。
维护Job的进度信息。
调度作业和任务分配给Groom服务器
分配执行的类和配置,整个Groom服务器。
为用户提供集群控制接口(Web和基于控制台)。
GroomServer:
GroomServer是一个process,通过BSPMaster启动BSP任务。每一个Groom都有BSPMaster通信,可以通过BSPMaster获取任务,报告状态。GroomServer在HDFS或者其他文件系统上运行,通常,GroomServer与与数据结点在一个物理结点上运行,以保证获得最佳性能。
Zookeeper:
Zookeeper用来管理BSPPeer的同步,用于实现BarrierSynchronisation机制。在ZK上,进入BSPPeer主要有进入Barrier和离开Barrier操作,所有进入Barrier的Peer会在zk上创建一个EPHEMERAL的node(/bsp/JobID/Superstep NO./TaskID),最后一个进入Barrier的Peer同时还会创建一个readynode(/bsp/JobID/Superstep NO./ready),Peer进入阻塞状态等待zk上所有task的node都删除后退出Barrier。
BSP Programming Model:
BSP(BulkSynchronous Parallel,整体同步并行计算模型)是英国计算机科学家Viliant在上世纪80年代提出的一种并行计算模型。Google发布的一往篇论文(《Pregel: A System for Large-Scale Graph Processing》)使得这一概念被更多人所认识,据说在Google 80%的程序运行在MapReduce上,20%的程序运行在Pregel上。和MapReduce一样,Google并没有开源Pregel,Apache按Pregel的思想提供了类似框架Hama。
以上
最后更新于